اُوپر،
ابواب:
1،
2،
3،
4،
5،
6،
7،
8
| اردو اصطلاح
|
English term
|
| مصفوفہ
|
Matrix
|
ریاضی میں مصفوفہ اعداد کے مجموعہ کو کہتے ہیں، جو قطاروں اور ستونوں میں سجائے جاتے ہیں۔ اعداد کی قطاریں بائیں سے دائیں جاتی ہیں، جبکہ ستون اوپر سے نیچے۔ مثال کہ طور پر نیچے لکھی مصفوفہ کی چار قطاریں اور تین ستون ہیں۔ ہم کہتے ہیں کہ اس مصفوفہ کا سائیز  ہے،اور مصفوفہ کے 12 اجزا ہیں۔
ہے،اور مصفوفہ کے 12 اجزا ہیں۔
![{\displaystyle \left[{\begin{matrix}1&3&2\\4&5&8\\12&6&9\\11&10&7\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad94eda1d82dac84fd1aa253d7f4f4b55a7d9d3)
ایک  مصفوفہ کو اس طرح لکھا جاتا ہے، یعنی m قطاریں اور n ستون،
مصفوفہ کو اس طرح لکھا جاتا ہے، یعنی m قطاریں اور n ستون،
![{\displaystyle A=\left[{\begin{matrix}a_{0,0}&a_{0,1}&\cdots &a_{0,n-1}\\a_{1,0}&a_{1,1}&\cdots &a_{1,n-1}\\\vdots &\vdots &\ddots &\vdots \\a_{m-1,0}&a_{m-1,1}&\cdots &a_{m-1,n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c600d126b26885f518c3a5089ff4c5002c4bcf4)
مصفوفہ جمع اور تفریق
[ترمیم]اگر دو مصفوفہ کو جمع کرنا ہو، تو دونوں کا سائیز برابر ہونا چاہیے۔ اسی طرح تفریق کے لیے بھی۔ نیچے جمع اور تفریق کی مثال دی ہے۔ ہر جز اپنے ہم منصب جز کے ساتھ جمع یا تفریق ہوتا ہے۔
![{\displaystyle \left[{\begin{matrix}8&-3&-2&1\\-1&1&4&5\\7&0&9&3\end{matrix}}\right]+\left[{\begin{matrix}2&3&4&1\\9&1&-4&3\\-8&1&6&7\end{matrix}}\right]=\left[{\begin{matrix}10&0&2&2\\8&2&0&8\\-1&1&15&10\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c20077960f773edaf30f41304e862c7b9de66f4)
![{\displaystyle \left[{\begin{matrix}8&-3&-2&1\\-1&1&4&5\\7&0&9&3\end{matrix}}\right]-\left[{\begin{matrix}2&3&4&1\\9&1&-4&3\\-8&1&6&7\end{matrix}}\right]=\left[{\begin{matrix}6&-6&-6&0\\-10&0&8&2\\15&-1&3&-4\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6989c6cee78b14fb51f5d37a4c23d6b1ca57ff0e)
دو مصفوفہوں کو ضرب دینے کے لیے پہلی مصفوفہ کے ستونوں کی تعداد دوسری مصفوفہ کی قطاروں کے برابر ہونی چاہیے۔ نیچے ہم مصفوفہ A کو مصفوفہ X سے ضرب دے کر مصفوفہ Y حاصل کرتے ہیں۔
![{\displaystyle A=\left[{\begin{matrix}a_{00}&a_{01}&a_{02}\\a_{10}&a_{11}&a_{12}\\a_{20}&a_{21}&a_{22}\end{matrix}}\right],X=\left[{\begin{matrix}x_{00}&x_{01}&x_{02}\\x_{10}&x_{11}&x_{12}\\x_{20}&x_{21}&x_{22}\end{matrix}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a99a3e7048b8e4d143e15ff0053651dc64ae718) یہاں دونوں مصفوفہ A اور X مربع مصفوفہ ہیں۔ دونوں کا سائیز
یہاں دونوں مصفوفہ A اور X مربع مصفوفہ ہیں۔ دونوں کا سائیز  ہے۔ اسلئے مصفوفہ Y کا سائیز بھی
ہے۔ اسلئے مصفوفہ Y کا سائیز بھی  ہو گا۔
ہو گا۔
![{\displaystyle Y=AX=\left[{\begin{matrix}y_{00}&y_{01}&y_{02}\\y_{10}&y_{11}&y_{12}\\y_{20}&y_{21}&y_{22}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6ce4724f7c3ae6b835a84e735f0da288bcd88d4)
![{\displaystyle Y=\left[{\begin{matrix}a_{00}x_{00}+a_{01}x_{10}+a_{02}x_{20}&a_{00}x_{01}+a_{01}x_{11}+a_{02}x_{21}&a_{00}x_{02}+a_{01}x_{12}+a_{02}x_{22}\\a_{10}x_{00}+a_{11}x_{10}+a_{12}x_{20}&a_{10}x_{01}+a_{11}x_{11}+a_{12}x_{21}&a_{10}x_{02}+a_{11}x_{12}+a_{12}x_{22}\\a_{20}x_{00}+a_{21}x_{10}+a_{22}x_{20}&a_{20}x_{01}+a_{21}x_{11}+a_{22}x_{21}&a_{20}x_{02}+a_{21}x_{12}+a_{22}x_{22}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1cb172e64e1920405fafe85beb13711c4e8b8d) غور کرنے پر معلوم ہو گا کہ مصفوفہ Y کا ہر جز، مصفوفہ A کی ایک قطار اور مصفوفہ X کے ایک ستون سے ٹکرا کر بنا ہے۔ مثال کے طور پر مصفوفہ Y کا جز
غور کرنے پر معلوم ہو گا کہ مصفوفہ Y کا ہر جز، مصفوفہ A کی ایک قطار اور مصفوفہ X کے ایک ستون سے ٹکرا کر بنا ہے۔ مثال کے طور پر مصفوفہ Y کا جز  مصفوفہ A کی قطار 0 اور مصفوفہ X کے ستون 0 کے ملاپ سے بنا ہے ۔ اسی طرح جز
مصفوفہ A کی قطار 0 اور مصفوفہ X کے ستون 0 کے ملاپ سے بنا ہے ۔ اسی طرح جز  مصفوفہ A کی قطار 1 اور مصفوفہ X کے ستون 2 کے ساتھ اس طرح بنا ہے:
مصفوفہ A کی قطار 1 اور مصفوفہ X کے ستون 2 کے ساتھ اس طرح بنا ہے:
![{\displaystyle y_{12}=\left[{\begin{matrix}a_{10}&a_{11}&a_{12}\end{matrix}}\right]\left[{\begin{matrix}x_{02}\\x_{12}\\x_{22}\end{matrix}}\right]=a_{10}x_{02}+a_{11}x_{12}+a_{12}x_{22}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5148cb02ddbd0b3e1a6607b69e8ec0fa2aa364a8) یک قطاری یا یک ستونی مصفوفہ کو سمتیہ (باب 4) بھی کہا جاتا ہے۔ ایک
یک قطاری یا یک ستونی مصفوفہ کو سمتیہ (باب 4) بھی کہا جاتا ہے۔ ایک  سائیز کی مصفوفہ کو ایک
سائیز کی مصفوفہ کو ایک  سائیز کی مصفوفہ سے ضرب دینے سے
سائیز کی مصفوفہ سے ضرب دینے سے  سائیز کی مصفوفہ نکلے گی۔ یاد رکھو کہ مصفوفہ ضرب میں عموماً
سائیز کی مصفوفہ نکلے گی۔ یاد رکھو کہ مصفوفہ ضرب میں عموماً 
شناخت مصفوفہ کو ریاضی میں خاص مقام حاصل ہے۔ یہ ایسی مصفوفہ ہے جس کے بائیں سے دائیں آر پار جز 1 ہوں، اور اس کے علاوہ باقی جز 0 ہوں۔ ایک  شناخت مصفوفہ کو یوں لکھیں گے:
شناخت مصفوفہ کو یوں لکھیں گے:
![{\displaystyle I_{n}=\left[{\begin{matrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a7139689aa8868f218ee3687a536c7be69a03a) شناخت مصفوفہ ہمیشہ مربع مصفوفہ ہوتی ہے۔ عام ریاضی میں یہ نمبر 1 سے مماثلت رکھتی ہے۔
شناخت مصفوفہ ہمیشہ مربع مصفوفہ ہوتی ہے۔ عام ریاضی میں یہ نمبر 1 سے مماثلت رکھتی ہے۔
مربع مصفوفہ کی طاقت بھی مصفوفہ ضرب کے ذریعہ تعریف ہوتی ہے، مثلاً  مربع مصفوفہ A کے لیے
مربع مصفوفہ A کے لیے

اس طرح کسی مثبت صحیح عدد  کے لیے
کے لیے

اور  کے لیے یہ شناخت مصفوفہ کے برابر ہو گا
کے لیے یہ شناخت مصفوفہ کے برابر ہو گا

مصفوفہ کا اُلٹ (مقلوب مصفوفہ)
[ترمیم]آپ سوچ رہے ہو گے کہ کیا مصفوفہ تقسیم بھی ممکن ہے؟ اسے سمجھنے کے لیے عام اعداد کی تقسیم پر غور کرو:
 یعنی عدد
یعنی عدد  کا الٹ عدد
کا الٹ عدد  ہے، ان دونوں اعداد کو ضرب دینے سے عدد 1 حاصل ہوتا ہے۔ اسی طرح
ہے، ان دونوں اعداد کو ضرب دینے سے عدد 1 حاصل ہوتا ہے۔ اسی طرح  سائیز کی مصفوفہ
سائیز کی مصفوفہ  کا الٹ مصفوفہ
کا الٹ مصفوفہ  ہو گی، جس کا سائیز بھی
ہو گی، جس کا سائیز بھی  ہو گا، جب ان دونوں مصفوفہوں کو ضرب دینے سے شناخت مصفوفہ حاصل ہو۔ یعنی
ہو گا، جب ان دونوں مصفوفہوں کو ضرب دینے سے شناخت مصفوفہ حاصل ہو۔ یعنی  صرف مربع مصفوفہ کا الٹ ممکن ہے، مگر ہر مربع مصفوفہ کا الٹ ممکن نہیں۔ جس مربع مصفوفہ کی قطاریں باہمی آزاد ہوں (اور ستون آپس میں باہمی آزاد ہوں)، صرف ایسی مصفوفہ کو الٹایا جا سکتا ہے۔ مثال کے طور پر مصفوفہ
صرف مربع مصفوفہ کا الٹ ممکن ہے، مگر ہر مربع مصفوفہ کا الٹ ممکن نہیں۔ جس مربع مصفوفہ کی قطاریں باہمی آزاد ہوں (اور ستون آپس میں باہمی آزاد ہوں)، صرف ایسی مصفوفہ کو الٹایا جا سکتا ہے۔ مثال کے طور پر مصفوفہ
![{\displaystyle \left[{\begin{matrix}1&-1&3\\-2&3&7\\-1&2&10\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff8523e46d0ef5149c01d232d7a8b885ebb515bf) کی تیسری قطار، پہلی دو قطاروں کو جمع کر کے بنی ہے، اس وجہ سے تیسری قطار پہلی دو قطاروں سے آزاد نہیں۔ اس لیے اس مصفوفہ کو الٹانا ممکن نہیں۔
کی تیسری قطار، پہلی دو قطاروں کو جمع کر کے بنی ہے، اس وجہ سے تیسری قطار پہلی دو قطاروں سے آزاد نہیں۔ اس لیے اس مصفوفہ کو الٹانا ممکن نہیں۔
مٰیٹرکس A، B، C، جن کا سائیز  ہو، اور r، s، عام عدد ہوں (
ہو، اور r، s، عام عدد ہوں ( یا
یا  میں) ، اور O ایک سائیز
میں) ، اور O ایک سائیز  کی مصفوفہ ہو جس کے تمام جُز صفر ہوں، تو مندرجہ ذیل سچ ہونگے
کی مصفوفہ ہو جس کے تمام جُز صفر ہوں، تو مندرجہ ذیل سچ ہونگے
- A + B = B + A
- (A + B) + C = A + (B + C)
- A + O = A
- A + (-A) = O
- (rs) A = r (sA)
- (r + s) A = rA + sA
- r (A + B) = rA + rB
- 1 A = A
اس سے یہ نتیجہ نکالا جا سکتا ہے کہ مصفوفہ جن کا سائیز ہو، اور ان کے جُز
ہو، اور ان کے جُز  یا
یا  میدان میں سے ہوں، کا مجموعہ سمتیہ فضا ہونے کی تمام شرائط پوری کرتا ہے۔
میدان میں سے ہوں، کا مجموعہ سمتیہ فضا ہونے کی تمام شرائط پوری کرتا ہے۔
اس کے علاوہ جب مصفوفہ کے سائیز ایسے ہوں کہ مصفوفہ ضرب ممکن ہو تو یہ سچ ہو گا (یاد رہے کہ ایک  مصفوفہ اور ایک
مصفوفہ اور ایک  مصفوفہ کی ضرب سے نکلنے والی مصفوفہ کا سائیز
مصفوفہ کی ضرب سے نکلنے والی مصفوفہ کا سائیز  ہوتا ہے)
ہوتا ہے)
- (AB)C = A(BC)
- A(B+C) = AB + AC
- (A+B)C = AC + BC
- r (AB) = (rA)B = A(rB)
مصفوفہ کا رتبہ اس میں باہمی لکیری آزاد قطاروں کی تعداد، یا اس میں باہمی لکیری آزاد ستونوں کی تعداد کو کہتے ہیں۔ ایک مصفوفہ کا زیادہ سے زیادہ رُتبہ اس کی قطاروں کی تعداد، یا ستونوں کی تعداد، (جو تعداد کم ہو) کے برابر ہو سکتا ہے۔
مصفوفہ ضرب بطور دالہ
[ترمیم]مصفوفہ ضرب لکیری دالہ بنانے میں کام آتی ہے۔ n رُخی فضا میں کسی بھی نقطہ کو n اصلی اعداد (میدان  ) پر مشتمل سمتیہ سے لکھا جاتا ہے۔ یعنی ہر نقطہ ایک
) پر مشتمل سمتیہ سے لکھا جاتا ہے۔ یعنی ہر نقطہ ایک  مصفوفہ کے بطور لکھا جا سکتا ہے۔ ہم کہتے ہیں کہ یہ نکات
مصفوفہ کے بطور لکھا جا سکتا ہے۔ ہم کہتے ہیں کہ یہ نکات  فضا میں ہیں۔ اس فضا کے ایک نقطہ X کو ہم یوں لکھ سکتے ہیں:
فضا میں ہیں۔ اس فضا کے ایک نقطہ X کو ہم یوں لکھ سکتے ہیں:
![{\displaystyle X=\left[{\begin{matrix}x_{0}\\x_{1}\\\vdots \\x_{n-1}\end{matrix}}\right]\,\,,\,x_{k}\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c85706436c952195f7a190b1219a7a73d16895)
اب اس نقطہ X کو ایک مصفوفہ A سے ضرب دے کر نقطہ Y حاصل ہوتا ہے۔ نقطہ Y، m رُخی فضا میں ہے۔ مصفوفہ ضرب دالہ کا کام کرتی ہے۔ دالہ کو عموماً  سے ظاہر کرتے ہیں:
سے ظاہر کرتے ہیں:

یا تفصیلاً
![{\displaystyle \left[{\begin{matrix}y_{0}\\y_{1}\\\vdots \\y_{m-1}\end{matrix}}\right]=\left[{\begin{matrix}a_{0,0}&a_{0,1}&\cdots &a_{0,n-1}\\a_{1,0}&a_{1,1}&\cdots &a_{1,n-1}\\\vdots &\vdots &\ddots &\vdots \\a_{m-1,0}&a_{m-1,1}&\cdots &a_{m-1,n-1}\\\end{matrix}}\right]\left[{\begin{matrix}x_{0}\\x_{1}\\\vdots \\x_{n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/303aa24e5ca409844c97d6140677ea4efaa70ab5)
اب یہ آسانی سے تسلی کی جا سکتی ہے کہ مصفوفہ ضرب ایک لکیری استحالہ کا کام کرتی ہے:

زیادہ دلچسپ صورت اس وقت ہوتی ہے جب مصفوفہ مربع ہو، یعنی نکات  سے
سے  میں جا رہے ہوں۔ اب ہم
میں جا رہے ہوں۔ اب ہم  سے
سے  کی مثال لیتے ہیں، یعنی مصفوفہ کا سائیز
کی مثال لیتے ہیں، یعنی مصفوفہ کا سائیز  ہے، اور یہ دو رُخی فضا، مثال کے
طور پر سکرین کی سطح کو ظاہر کرتی ہے۔
ہے، اور یہ دو رُخی فضا، مثال کے
طور پر سکرین کی سطح کو ظاہر کرتی ہے۔
مصفوفہ
![{\displaystyle A=\left[{\begin{matrix}2&1\\0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c10e04f4f9fea2b2e65e469d0c5a00e41c2ec1fd) سکرین پر عمودی (vertical) لکیروں کو ترچھا کرتی ہے، اور ان کے درمیان فاصلے بڑھاتی ہے، جبکہ مصفوفہ
سکرین پر عمودی (vertical) لکیروں کو ترچھا کرتی ہے، اور ان کے درمیان فاصلے بڑھاتی ہے، جبکہ مصفوفہ
![{\displaystyle A=\left[{\begin{matrix}1&0\\1&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2616235de34993fc1b636ce18ed01bf514157716) سکرین پر افقی (horizontal) لکیروں کو ترچھا کرتی ہے، اور ان کے درمیان فاصلے بڑھاتی ہے۔ جبکہ مصفوفہ
سکرین پر افقی (horizontal) لکیروں کو ترچھا کرتی ہے، اور ان کے درمیان فاصلے بڑھاتی ہے۔ جبکہ مصفوفہ
![{\displaystyle A=\left[{\begin{matrix}2&1\\1&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a65fe80634f7d0262c09ac649d1c955a5319307) دونوں اطراف کی لکیروں کو ترچھا کرتی ہے۔
دونوں اطراف کی لکیروں کو ترچھا کرتی ہے۔
![{\displaystyle \left[{\begin{matrix}y_{0}\\y_{1}\end{matrix}}\right]=f\left(\left[{\begin{matrix}x_{0}\\x_{1}\end{matrix}}\right]\right)=\left[{\begin{matrix}2&1\\1&2\end{matrix}}\right]\left[{\begin{matrix}x_{0}\\x_{1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67c0cef5e425a02a213c8f5fc031d3ce20436b37)
ملاحظہ ہو۔ پہلی تصویر (نیلا رنگ) میں مربع تانا بانا دکھایا گیا ہے۔ ان نکات کو مصفوفہ سے ضرب دے کر دوسری تصویر (سرخ رنگ) میں ترچھے تانا بانا حاصل ہوتا ہے۔ دیکھو کہ ایک مربع بدل جاتا ہے پیرللوگرام (parallelogram) میں ( تصاویر میں کالے ڈبے)۔
مصفوفہ ضرب بطور لکیری دالہ
 |
 |
 |
اگر پہلی تصویر میں دالہ کے ساحہ (domain) کے کالے ڈبے کے نکات S کو کہا جائے، تو دوسری تصویر میں دالہ کے حیطہ (range) میں کالے ڈبے کے نکات f(S) ہوں گے۔ ان دونوں کالے ڈبوں کا رقبہ مصفوفہ A کے دترمینان (باب 3) کی تناسب سے ہوتا ہے:

تجزیہ نہیں کر پایا (PNG یا SVG کے ساتھ MathML (جدید براؤزر وغیرہ کے لیے اسے استعمال کرنے کی سفارش کی جاتی ہے): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/ur.wikibooks.org/v1/":): {\displaystyle صیغہ یہاں درج کیجئے}
=== مثال: گھماؤ===
گھماؤ مصفوفہ
![{\displaystyle A=\left[{\begin{matrix}\cos(\theta )&-\sin(\theta )\\\sin(\theta )&\cos(\theta )\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09a5358c575cf71a93c9a7ba1fb0a68d40bb6e8b)
 میں نکات کو مبدا (origin) کے گرد زاویہ
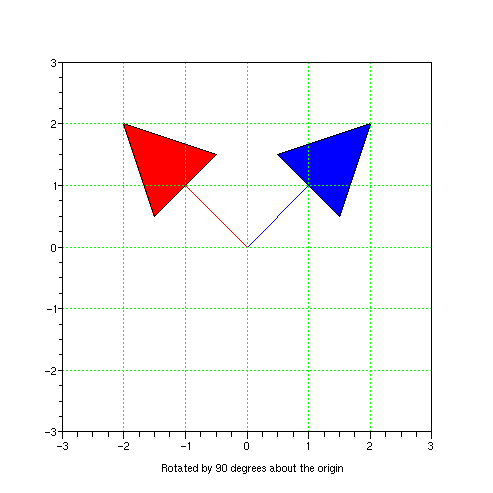
میں نکات کو مبدا (origin) کے گرد زاویہ  سے اُلٹی گھڑی کی سمت گھما دیتی ہے۔ ملاحظہ ہو
سے اُلٹی گھڑی کی سمت گھما دیتی ہے۔ ملاحظہ ہو  کے لیے 90 درجے کے زاویہ سے مبداء کے گِرد گھمانا (مبداء سے مراد نکتہ (0,0) ہے)۔ تصویر میں نیلے رنگ کے نکات کو مصفوفہ سے ضرب دے کر سرخ رنگ کے نکات حاصل ہوتے ہیں۔
کے لیے 90 درجے کے زاویہ سے مبداء کے گِرد گھمانا (مبداء سے مراد نکتہ (0,0) ہے)۔ تصویر میں نیلے رنگ کے نکات کو مصفوفہ سے ضرب دے کر سرخ رنگ کے نکات حاصل ہوتے ہیں۔
نوٹ: تصاویر کا W:ur:سائیلیب سکرپٹ دیکھنے کے لیے تصاویر پر کلک کرو۔
 یہاں ریاضی مساوات کو بائیں سے دائیں (LTR) پڑھو ریاضی علامات
یہاں ریاضی مساوات کو بائیں سے دائیں (LTR) پڑھو ریاضی علامات
اُوپر،
ابواب:
1،
2،
3،
4،
5،
6،
7،
8




![{\displaystyle \left[{\begin{matrix}1&3&2\\4&5&8\\12&6&9\\11&10&7\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad94eda1d82dac84fd1aa253d7f4f4b55a7d9d3)

![{\displaystyle A=\left[{\begin{matrix}a_{0,0}&a_{0,1}&\cdots &a_{0,n-1}\\a_{1,0}&a_{1,1}&\cdots &a_{1,n-1}\\\vdots &\vdots &\ddots &\vdots \\a_{m-1,0}&a_{m-1,1}&\cdots &a_{m-1,n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c600d126b26885f518c3a5089ff4c5002c4bcf4)
![{\displaystyle \left[{\begin{matrix}8&-3&-2&1\\-1&1&4&5\\7&0&9&3\end{matrix}}\right]+\left[{\begin{matrix}2&3&4&1\\9&1&-4&3\\-8&1&6&7\end{matrix}}\right]=\left[{\begin{matrix}10&0&2&2\\8&2&0&8\\-1&1&15&10\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c20077960f773edaf30f41304e862c7b9de66f4)
![{\displaystyle \left[{\begin{matrix}8&-3&-2&1\\-1&1&4&5\\7&0&9&3\end{matrix}}\right]-\left[{\begin{matrix}2&3&4&1\\9&1&-4&3\\-8&1&6&7\end{matrix}}\right]=\left[{\begin{matrix}6&-6&-6&0\\-10&0&8&2\\15&-1&3&-4\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6989c6cee78b14fb51f5d37a4c23d6b1ca57ff0e)
![{\displaystyle A=\left[{\begin{matrix}a_{00}&a_{01}&a_{02}\\a_{10}&a_{11}&a_{12}\\a_{20}&a_{21}&a_{22}\end{matrix}}\right],X=\left[{\begin{matrix}x_{00}&x_{01}&x_{02}\\x_{10}&x_{11}&x_{12}\\x_{20}&x_{21}&x_{22}\end{matrix}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a99a3e7048b8e4d143e15ff0053651dc64ae718)

![{\displaystyle Y=AX=\left[{\begin{matrix}y_{00}&y_{01}&y_{02}\\y_{10}&y_{11}&y_{12}\\y_{20}&y_{21}&y_{22}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6ce4724f7c3ae6b835a84e735f0da288bcd88d4)
![{\displaystyle Y=\left[{\begin{matrix}a_{00}x_{00}+a_{01}x_{10}+a_{02}x_{20}&a_{00}x_{01}+a_{01}x_{11}+a_{02}x_{21}&a_{00}x_{02}+a_{01}x_{12}+a_{02}x_{22}\\a_{10}x_{00}+a_{11}x_{10}+a_{12}x_{20}&a_{10}x_{01}+a_{11}x_{11}+a_{12}x_{21}&a_{10}x_{02}+a_{11}x_{12}+a_{12}x_{22}\\a_{20}x_{00}+a_{21}x_{10}+a_{22}x_{20}&a_{20}x_{01}+a_{21}x_{11}+a_{22}x_{21}&a_{20}x_{02}+a_{21}x_{12}+a_{22}x_{22}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1cb172e64e1920405fafe85beb13711c4e8b8d)


![{\displaystyle y_{12}=\left[{\begin{matrix}a_{10}&a_{11}&a_{12}\end{matrix}}\right]\left[{\begin{matrix}x_{02}\\x_{12}\\x_{22}\end{matrix}}\right]=a_{10}x_{02}+a_{11}x_{12}+a_{12}x_{22}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5148cb02ddbd0b3e1a6607b69e8ec0fa2aa364a8)




![{\displaystyle I_{n}=\left[{\begin{matrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a7139689aa8868f218ee3687a536c7be69a03a)












![{\displaystyle \left[{\begin{matrix}1&-1&3\\-2&3&7\\-1&2&10\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff8523e46d0ef5149c01d232d7a8b885ebb515bf)






![{\displaystyle X=\left[{\begin{matrix}x_{0}\\x_{1}\\\vdots \\x_{n-1}\end{matrix}}\right]\,\,,\,x_{k}\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c85706436c952195f7a190b1219a7a73d16895)


![{\displaystyle \left[{\begin{matrix}y_{0}\\y_{1}\\\vdots \\y_{m-1}\end{matrix}}\right]=\left[{\begin{matrix}a_{0,0}&a_{0,1}&\cdots &a_{0,n-1}\\a_{1,0}&a_{1,1}&\cdots &a_{1,n-1}\\\vdots &\vdots &\ddots &\vdots \\a_{m-1,0}&a_{m-1,1}&\cdots &a_{m-1,n-1}\\\end{matrix}}\right]\left[{\begin{matrix}x_{0}\\x_{1}\\\vdots \\x_{n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/303aa24e5ca409844c97d6140677ea4efaa70ab5)



![{\displaystyle A=\left[{\begin{matrix}2&1\\0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c10e04f4f9fea2b2e65e469d0c5a00e41c2ec1fd)
![{\displaystyle A=\left[{\begin{matrix}1&0\\1&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2616235de34993fc1b636ce18ed01bf514157716)
![{\displaystyle A=\left[{\begin{matrix}2&1\\1&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a65fe80634f7d0262c09ac649d1c955a5319307)
![{\displaystyle \left[{\begin{matrix}y_{0}\\y_{1}\end{matrix}}\right]=f\left(\left[{\begin{matrix}x_{0}\\x_{1}\end{matrix}}\right]\right)=\left[{\begin{matrix}2&1\\1&2\end{matrix}}\right]\left[{\begin{matrix}x_{0}\\x_{1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67c0cef5e425a02a213c8f5fc031d3ce20436b37)


![{\displaystyle A=\left[{\begin{matrix}\cos(\theta )&-\sin(\theta )\\\sin(\theta )&\cos(\theta )\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09a5358c575cf71a93c9a7ba1fb0a68d40bb6e8b)




